[В работе] Конспект лекции по раскраскам
Отправьте статью сегодня! Журнал выйдет 2 ноября , печатный экземпляр отправим 6 ноября. Автор : Моторина Екатерина Алексеевна. Дата публикации : Статья просмотрена: раз. Моторина, Е.

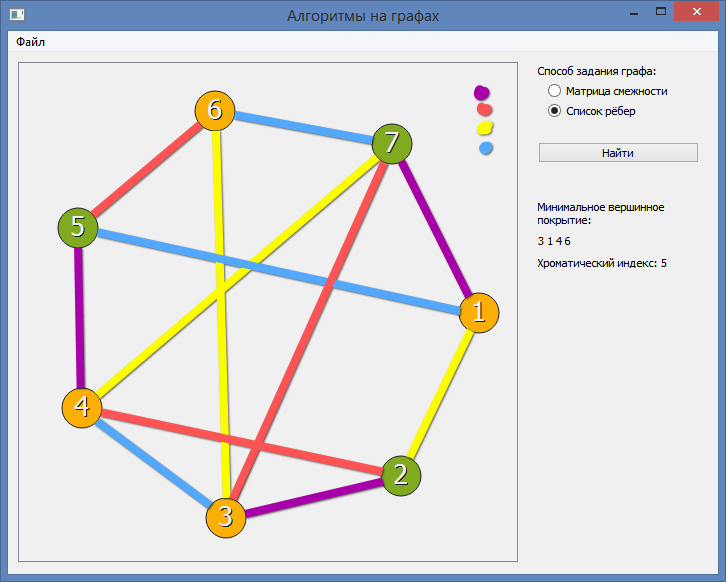

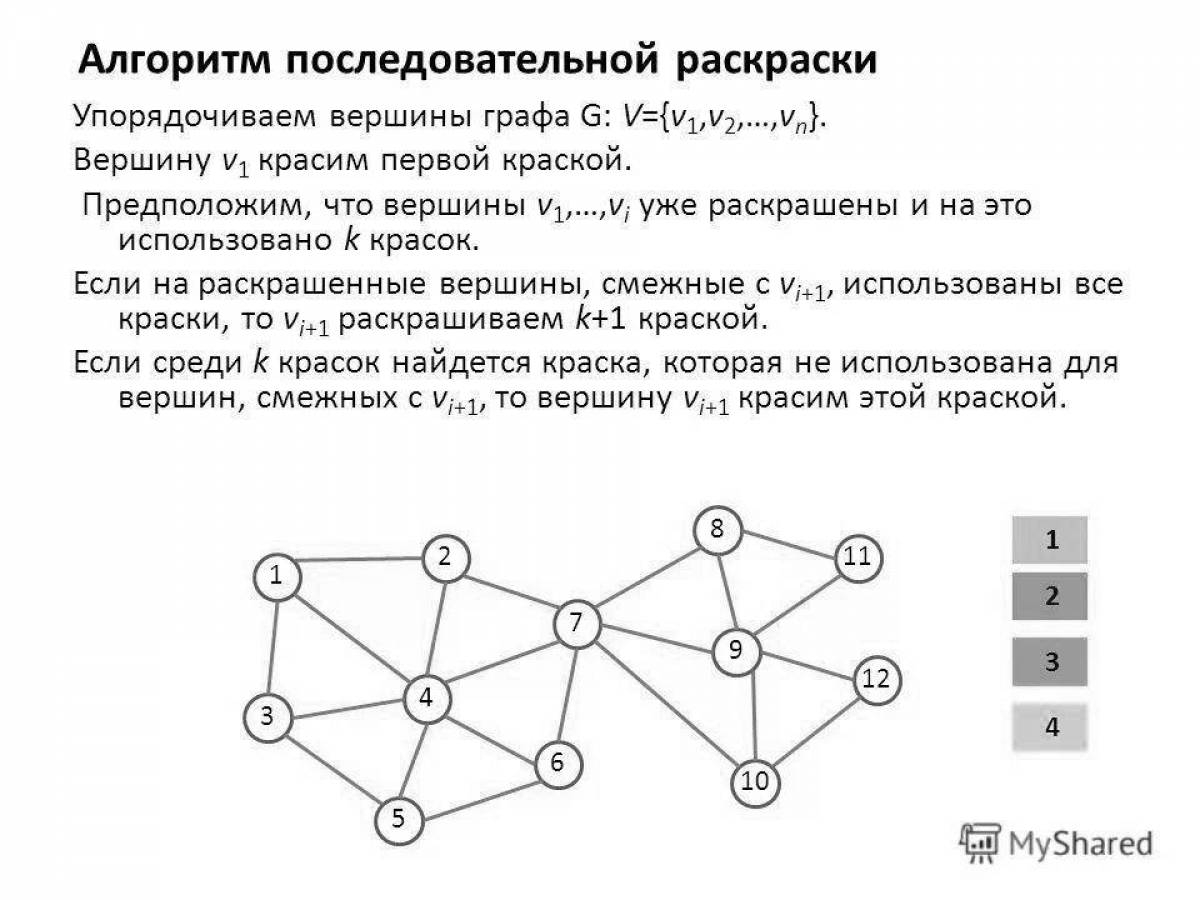




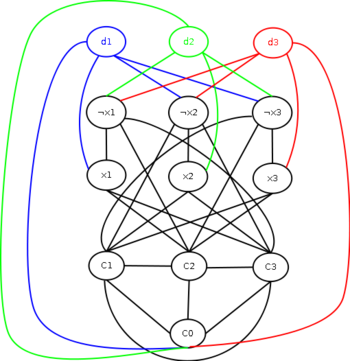
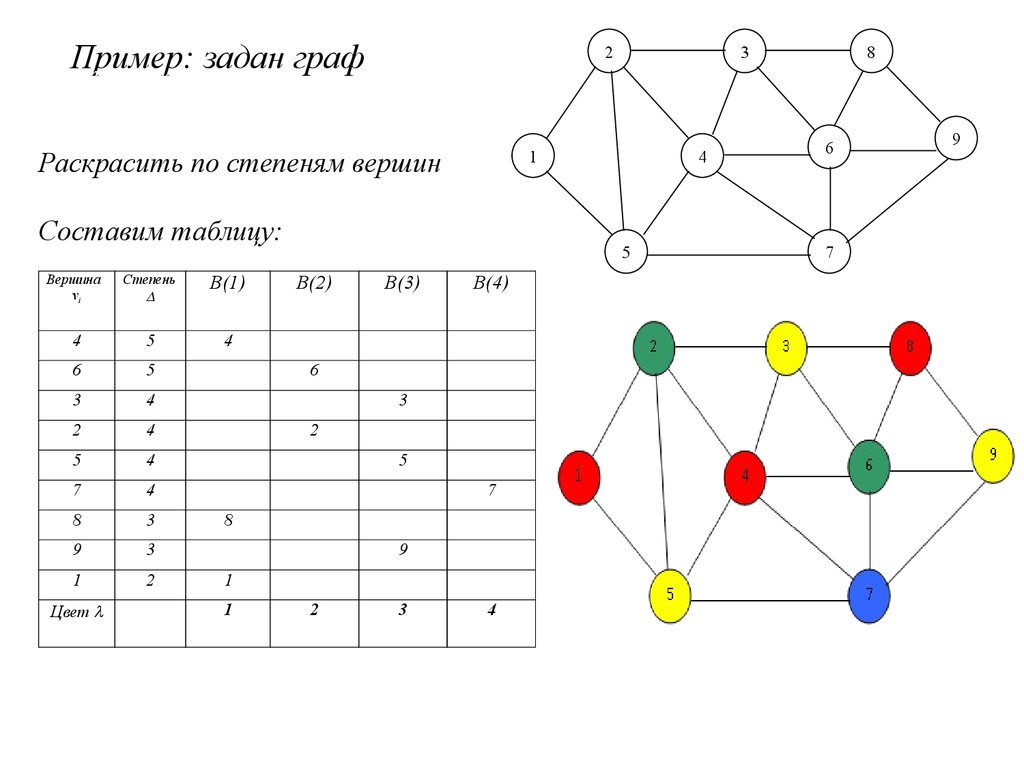
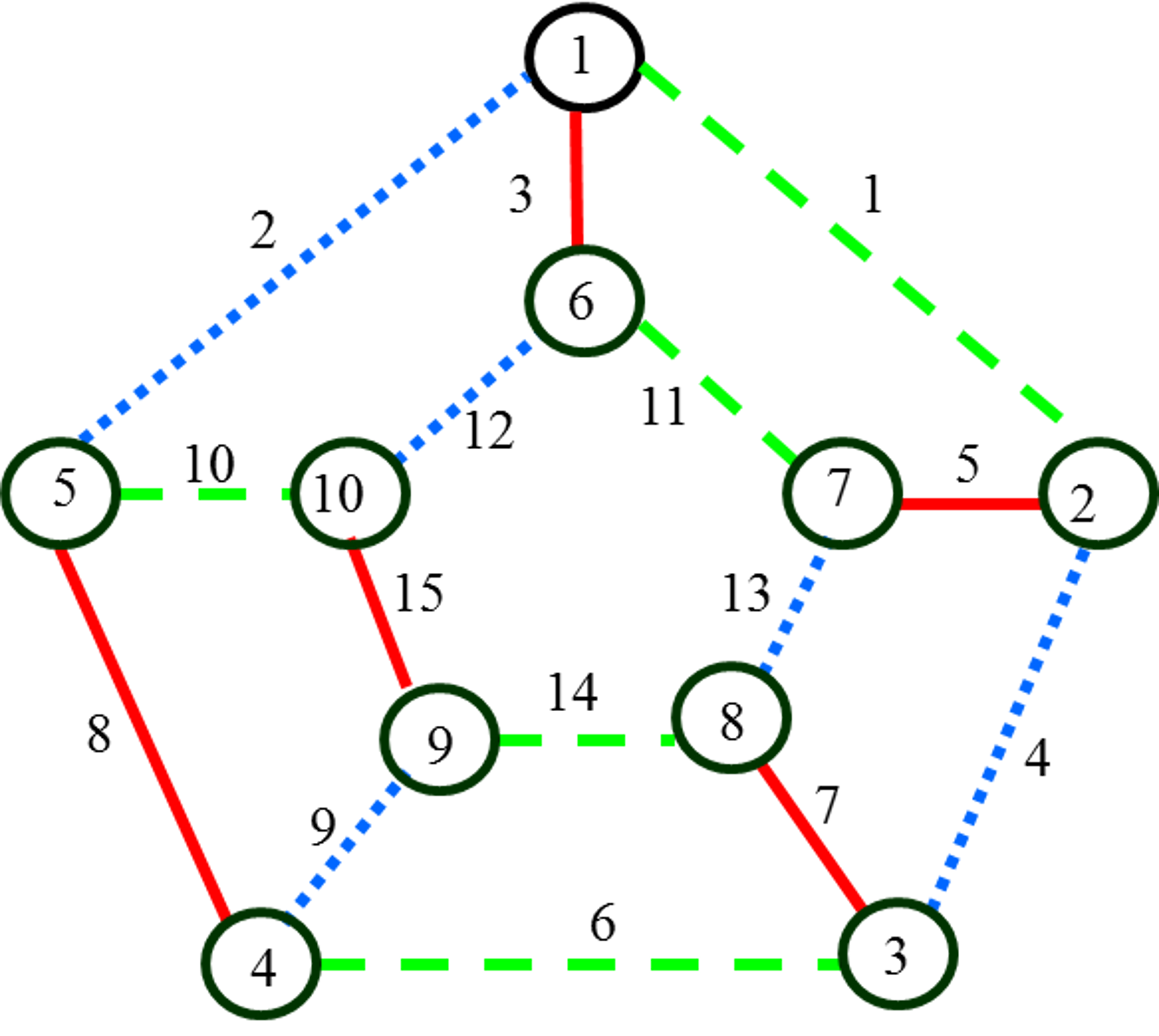
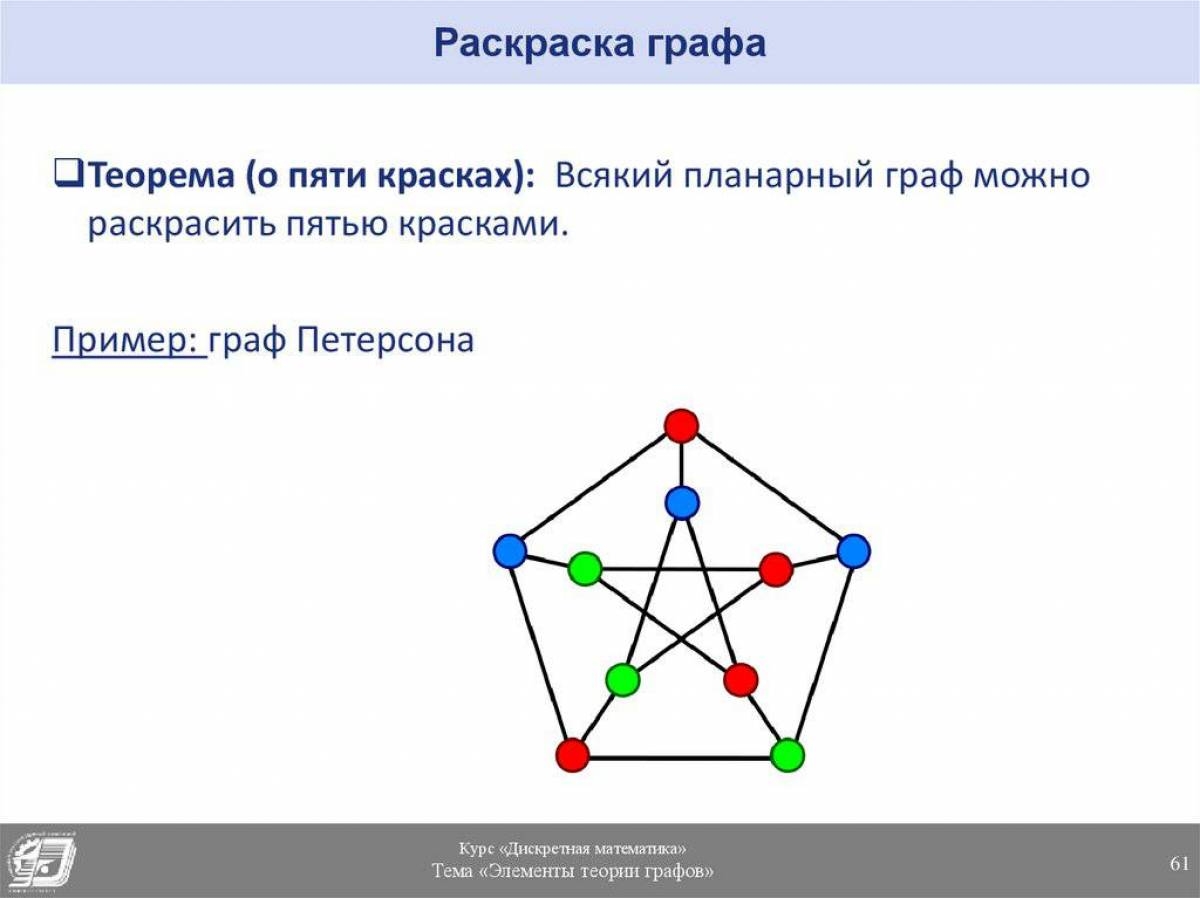
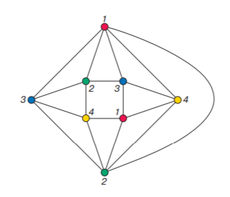
Когда говорят о раскраске графов, почти всегда подразумевают под этим раскраску их вершин, то есть присвоение цветовых меток вершинам графа так, чтобы любые две вершины, имеющие общее ребро, имели разные цвета. Так как графы, в которых есть петли, не могут быть раскрашены таким образом, они не являются предметом обсуждения. Полный граф - такой граф, у которого есть путь из каждой вершины в каждую. Очевидно, что хроматическое число полного графа совпадает с количеством вершин. Пусть дан граф и дана его раскраска. Чтобы проверить её корректность, нужно обойти все ребра и проверить, если одинаковые цвета на концах.
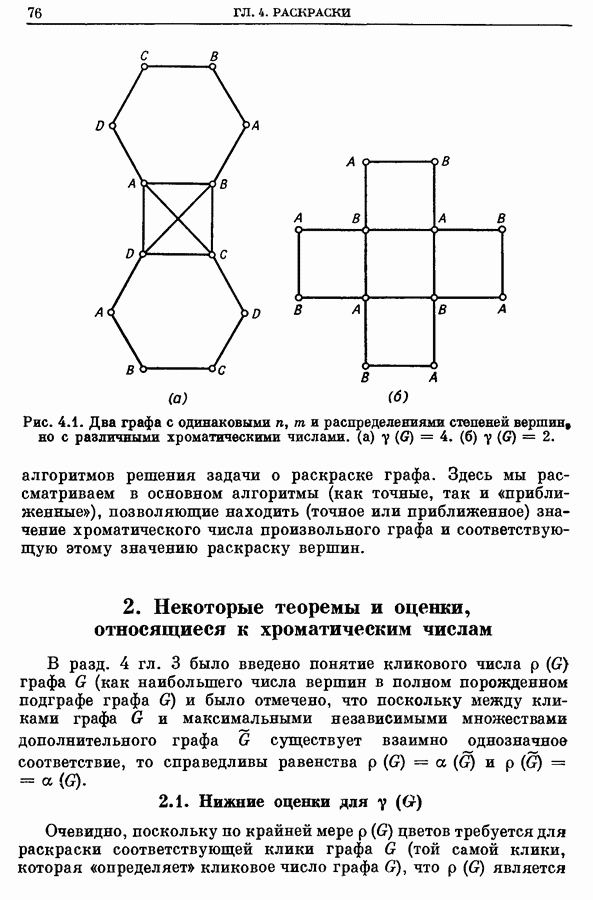





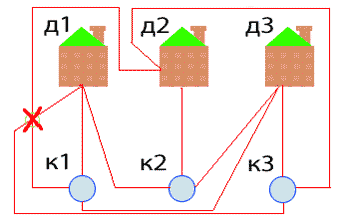
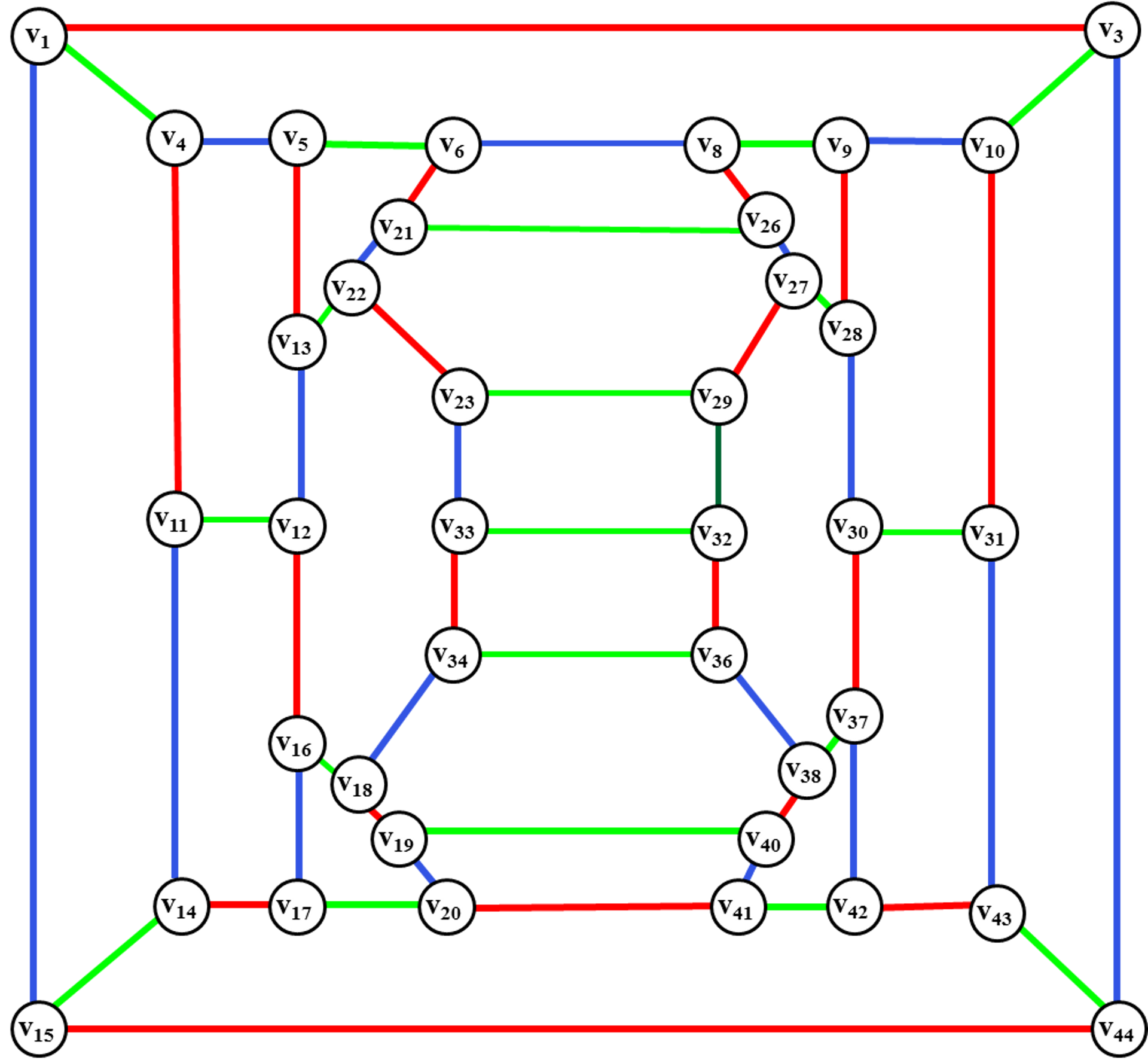
При решении практических задач с применением графов возникает необходимость в разбиении множества вершин графа на классы попарно несмежных между вершин. Довольно часто дополнительно требуется, чтобы таких классов было наименьшее число. В теории графов подобные задачи формулируются в терминах раскраски вершин графа. Привести пример графа, не имеющего треугольников, то есть трехэлементных полных подграфов, у которых хроматическое число равно 5.